Вектора, определения
Вектор - это направленный прямолинейный отрезок, т.е. отрезок, имеющий длину и определенное направление. Графически вектор обозначается отрезком прямой, на котором ставится стрелка, указывающая направление вектора, в частности могут указываться начало и конец вектора, например А - начало вектора, в В - конец вектора. Свойства векторов Вы найдете чуть ниже. Будем обозначать вектор одной буквой с черточкой над ней или буквами начала и конца вектора, также с чертой над ними.
Свойства векторов
1°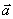 
+ 
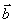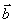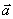= + - коммутативность;
2° + ( +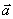 
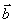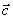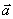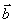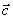) = ( + ) + - ассоциативность (по сложению);
3° +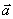 
= ;
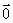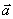4° 1 × = ;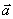
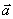5° 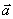+ (-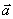) = 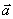- 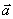= 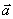+ (-1) = ;
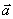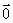6° α(β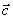) = (αβ) 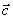- ассоциативность (по отношению к числам);
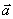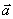7° (α + β) = α + β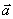 - дистрибутивность (по отношению к умножению на вектор);
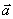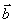8° α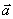( + ) = α + α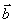 - дистрибутивность (по отношению к умножению на число).
α, β - числа.
Свойства векторов незаменимы при сложении, вычитании векторов, при умножении векторов и умножении вектора на число, при упрощении выражений, при нахождении скалярного и векторного произведений векторов и много другого. Свойства векторов очень просты к пониманию и легки к запоминанию, но не зная свойства векторов в университете будет очень сложно...
